The deadlines do not apply to the Bonus questions,
which expire only once we solve them in class, or on November 28 at
latest.
Notation: 5.1/8a means exercise 8, part a, in chapter 5,
section 1.
| No. |
Date due: |
Problems: |
| 14 |
We Nov 28 |
Bonus question:
4.5/4b
|
| 13 |
Mo Nov 19 |
3.4/4c Use Mike Copley's Java applet
to build a heap (note: it does not take negative numbers, so you have
to "cheat") then apply the algorithm described in the book and
shown in Figure 3.25 to sort the heap. Warning: the procedure will be different
from what is shown by the applet, so only execute the first stage of
it. Show each stage of the heap while it is being sorted. Perform the
algorithm only for the list given in 3.4/1b.
4.3/16: only set up the network, do not solve.
Board problems:
- Use merge sort to sort the list 5,1,4,3,2. Show all phases.
- Use bubble sort to sort the list 4,1,3,5. Show all phases.
Bonus question:
Let r1, r2, ...,
rn, and c1,
c2, ..., cn be non-negative
integers such that the sum of the ri's is the same
as the sum of the cj's. Prove that, using the
"northwest corner method", described in Section 4.5, it is
possible to find an n x n matrix with non-negative integer
entries such that the sum of the entries in the i-th row is
ri, and the sum of the entries in the j-th
column is cj.
|
| 12 |
We Nov 14 |
3.3/6
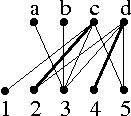
Board problem: Find a maximum matching and a minimum cover for
the bipartite graph shown in the picture, by converting the problem to a
network flow question and solving it. Start with the partial matching
consisting of the edges 2c and 4d (shown in bold).
 Bonus problem: Find a weighted graph and a selected edge for
which exploring the cheaper lower bound following the "branch and
bound" method makes you choose a branch containing only non-optimal
Hamiltonian cycles (thus forcing you to backtrack).
Bonus problem: Find a weighted graph and a selected edge for
which exploring the cheaper lower bound following the "branch and
bound" method makes you choose a branch containing only non-optimal
Hamiltonian cycles (thus forcing you to backtrack).
|
| 11 |
We Nov 14 |
3.3/2
|
| 10 |
We Oct 31 |
4.4/2.
Our second test is on Monday, October 29. You may download
the Sample Test 2 to prepare.
|
| 9 |
We Oct 24 |
3.2/20 (reassigned with more hints); 4.3/2, 6, 10.
|
| 8 |
We Oct 17 |
4.2/2,4,8.
|
| 7 |
We Oct 10 |
3.2/2, 4, 12ab (for part a, use answer to 17), 20, 24; 4.1/2ab, 4
Bonus problems:
- How can you find the degree of a vertex using the adjacency
matrix? (Justify your answer.)
- 4.1/8
|
| 6 |
We Oct 3 |
3.1/2, 4, 6, 10, 16.
|
| 5 |
Mo Sep 24 |
2.4/4, 8, 14.
Note:
2.4/8a has a typo. The correct inequality is:
 . .
Our first test is on Monday, September 24. You may download
the Sample Test 1 to prepare.
Bonus: Show that every tournament has a " king", i.e. a
team k such that for each other team t there is a
directed path of length at most two from k to t.
|
| 4 |
Mo Sep 17 |
2.2/2ac, 4ado, 6, 16 (use Grinbergs' theorem); 2.3/2ae, 8ab.
|
| 3 |
We Sep 12 |
1.4/20; 2.1/2,4,10.
|
| 2 |
We Sep 5 |
1.3/2, 4, 10, 14; 1.4/2,4,8
Board problem: The Petersen graph is shown in the picture below.
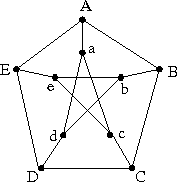 Show that the Petersen graph may also be defined as the graph whose
vertices are all 2-element subsets of {1,2,3,4,5} with
an edge connecting {i,j} and {k,l} exactly when
{i,j} and {k,l} are disjoint.
Show that the Petersen graph may also be defined as the graph whose
vertices are all 2-element subsets of {1,2,3,4,5} with
an edge connecting {i,j} and {k,l} exactly when
{i,j} and {k,l} are disjoint.
Bonus problems:
- Prove that the edge graph of the n-dimensional hypercube is
bipartite. (The vertices of the n-dimensional hypercube are all
01-strings of length n, two vertices are adjacent when exactly
one of their coordinates differs.)
- Generalize Euler's formula to non-connected planar graphs (introduce a
variable c for the number of connected components.
- Show that allowing disconnected countries no fixed number of colors
suffices to color all maps.
|
| 1 |
Mo Aug 27 |
1.1/2ab, 6a, 8, 16a; 1.2/2, 4, 6aeg.
|

 .
.
