ARCHIVE PAGE

This page is not updated any more.

Homework assignments
(MATH 3116-001, Fall 2009)
Instructor: Gábor Hetyei Last update: Monday, November 30, 2009

Disclaimer: The information below comes with no warranty. If, due to typographical error, there is a discrepancy between the exercises announced in class and the ones below, or this page is not completely up to date, the required homework consists of those exercises which were announced in class. Check for the time of last update above. If, by my mistake, a wrong exercise shows up below, I will allow you extra time to hand in the exercise that was announced in class. If, however, exercises are missing because this page is not up to date, it is your responsibility to contact me before the due date. (No extra time will be allowed in that case.) This page is up to date if the last update happened after the last class before the next due date.

The deadlines do not apply to the Bonus questions, which expire only once we solve them in class, or on November 28 at latest.

Notation: 5.1/8a means exercise 8, part a, in chapter 5, section 1.

No. Date due: Problems:
13 Mo Dec 7 3.4/4c Use Mike Copley's Java applet to build a heap (note: it does not take negative numbers, so you have to "cheat") then apply the algorithm described in the book and shown in Figure 3.25 to sort the heap. Warning: the procedure will be different from what is shown by the applet, so only execute the first stage of it. Show each stage of the heap while it is being sorted. Perform the algorithm only for the list given in 3.4/1b.
Board problem: Use bubble sort to sort the list 5,1,3,4,2. Show all phases.
12 Mo Nov 30 4.4/8.
Bonus problems:
  1. State a linear programming problem whose integer valued solution finds a maximum matching in a bipartite graph. Show that the dual problem is related to finding a minimum edge cover. You may use the Linear Programming entry on Wikipedia as your reference.
  2. Prove that an n by n permutation matrix can not be written as the convex combination of other n permutation matrices.
11 Mo Nov 23 4.5/4b.
10 We Nov 11 4.4/2 (all of part b, for part a outline only how you would set up the network).
9 We Oct 28 4.3/2b,6.
8 We Oct 21 4.2/2,4,8.
7 Mo Oct 19 3.1/29ac;   3.2/2,4,12ab (use 17 for 12a), 20,24;   4.1/2ab, 4.
Bonus problems:
  1. How can you find the degree of a vertex using the adjacency matrix? (Justify your answer.)
  2. Consider the following variant of the pitcher pouring puzzle. There are three bottles, of sizes 8 liters, 5 liters and 3 liters. Originally the 8 liter bottle is full, the other two are empty. A valid move consists of pouring wine from one bottle into the other, until the pouring bottle becomes empty or the receiving bottle becomes full. Use a geometric argument to describe the set of configurations that can be reached from the starting configuration.
6 We Oct 7 3.1/2,4,6,16.
5 We Sep 30 1.4/18   2.4/4, 8, 14.
Note: 2.4/8a has a typo. The correct inequality is:
.

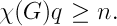Our first test is on Monday September 28. You may downloand the Sample Test 1 I will distribute on Wednesday September 23.
4 We Sep 23 2.2/2ac, 4ado, 6, 16 (use Grinberg's theorem);   2.3/2ae, 8ab.
Board problem: What is the chromatic number of the wheel graph with n+1 vertices? (Example 2.3 in Section 2.3 answers the question for n=6. You need to generalize that example. A wheel graph on n+1 vertices has one vertex in the center, connected to all other vertices. The vertices that are different from the center form a circuit of length n.)
3 We Sep 16 1.4/20;  2.1/2,4,10.
2 We Sep 16 1.3/2, 4, 10, 14   1.4/2,4,8.
Board problem: The Petersen graph is shown in the picture below.
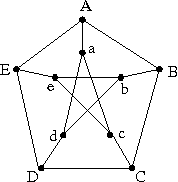
Show that the Petersen graph may also be defined as the graph whose vertices are all 2-element subsets of {1,2,3,4,5} with an edge connecting {i,j} and {k,l} exactly when {i,j} and {k,l} are disjoint.
Bonus problems:
  1. Prove that the edge graph of the n-dimensional hypercube is bipartite. (The vertices of the n-dimensional hypercube are all 01-strings of length n, two vertices are adjacent when exactly one of their coordinates differs.)
  2. Generalize Euler's formula to non-connected planar graphs (introduce a variable c for the number of connected components.
  3. Show that allowing disconnected countries no fixed number of colors suffices to color all maps.
1 We Sep 2 1.1/2ab, 6a, 8, 16a;   1.2/2, 4, 6aeg.