ARCHIVE PAGE

This page is not updated any more.

Homework assignments
(MATH 3116-001, Fall 2013)
Instructor: Gábor Hetyei Last update: Sunday, December 1, 2013

Disclaimer: The information below comes with no warranty. If, due to typographical error, there is a discrepancy between the exercises announced in class and the ones below, or this page is not completely up to date, the required homework consists of those exercises which were announced in class. Check for the time of last update above. If, by my mistake, a wrong exercise shows up below, I will allow you extra time to hand in the exercise that was announced in class. If, however, exercises are missing because this page is not up to date, it is your responsibility to contact me before the due date. (No extra time will be allowed in that case.) This page is up to date if the last update happened after the last class before the next due date.

The deadlines do not apply to the Bonus questions, which expire only once we solve them in class, or on November 28 at latest.

Notation: 5.1/8a means exercise 8, part a, in chapter 5, section 1.

No. Date due: Problems:
There will be no more homework assigned in this class. I will discuss the bonus problem solutions on Monday December 2. Our final exam will be on Monday, December 9. You may download the Sample Final Exam Questions to prepare for it.
13 Mo Nov 25 4.3/16, 3.3/2 (the second one will not be graded).
12 We Nov 20 4.5/4b.
11 We Nov 13 4.4/8
Board problem: Write the doubly stochastic matrix
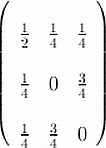
as a convex combination of permutation matrices.
Bonus question: Prove that no permutation matrix is the convex combination of other permutation matrices.
10 We Nov 6 4.4/2b.
9 We Oct 30 4.3/6,9. For these exercises, explain how you would set up the corresponding network flow problem. Find a maximum flow and minimum cut (you do not have to provide the details on that) and then explain how your solution answers the orginal question.
Our second test is on Wednesday October 30. You may download the Sample Test 2 to prepare for it.
8 We Oct 23 4.2/2,4,8;   4.3/2b
7 We Oct 16 4.1/2ab, 4a.
Bonus question: 4.1/8
6 We Oct 9 1.4/18;   3.1/16;   3.2/2, 12ab, 20; 3.4/4c.
For 3.4/c you should use Mike Copley's Java applet to build a heap (note: it does not take negative numbers, so you have to "cheat"). Then apply the algorithm described in the book and shown in Figure 3.25 to sort the heap. Warning: the procedure in our book to sort the heap is different from what is shown by the applet, so only use the applet to build the heap. Show each stage of the heap while it is being sorted.
Board problem: Use bubble sort to sort the list 5,1,3,4,2. Show all phases.
5 We Oct 2 3.1/2,6,31ac.
4 We Sep 25 2.4/4,8,14abcd.
Bonus problems:
  1. Show that, allowing disconnected countries, no fixed number of colors suffices to color all maps.
  2. Prove Grinberg's theorem (Section 2.2, Theorem 3).
  3. Find and prove a formula for the chromatic polynomial of a circuit Cn of length n.
3 We Sep 18 2.2/2ac, 4bcp, 16;   2.3/2ab, 10ab.
2 We Sep 11 2.1/2,4,10;   1.4/2,8,20.
Bonus problem (2pts), expires when this assignment is due: Find the theorem in the book (page number, theorem number) stating the number of edges of a tree.
1 We Sep 4 1.1/2ab, 6a, 8, 16a;   1.2/2,4,6bfh;   1.3/2,6,12a.
Bonus questions:
  1. 1.2/6e
  2. Prove that the edge graph of the n-dimensional hypercube is bipartite. (The vertices of the n-dimensional hypercube are all 01-strings of length n, two vertices are adjacent when exactly one of their coordinates differs.)