ARCHIVE PAGE

This page is not updated any more.

Homework assignments
(MATH 3116-001, Fall 2017)
Instructor: Gábor Hetyei Last update: Thursday, November 16, 2017

Disclaimer: The information below comes with no warranty. If, due to typographical error, there is a discrepancy between the exercises announced in class and the ones below, or this page is not completely up to date, the required homework consists of those exercises which were announced in class. Check for the time of last update above. If, by my mistake, a wrong exercise shows up below, I will allow you extra time to hand in the exercise that was announced in class. If, however, exercises are missing because this page is not up to date, it is your responsibility to contact me before the due date. (No extra time will be allowed in that case.) This page is up to date if the last update happened after the last class before the next due date.

The deadlines do not apply to the Bonus questions, which expire only once we solve them in class, or on November 29 at latest.

Notation: 5.1/8a means exercise 8, part a, in chapter 5, section 1.

No. Date due: Problems:
10 Mo Nov 20 4.3/16   4.4/8.
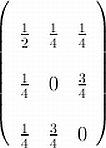
Board problem: Write the doubly stochastic matrix
as a convex combination of permutation matrices.
9 Mo Nov 13 4.3/2b (show all steps, augmenting paths, slack graphs, final flow and minimum cut), 6 (just final answer, together with conclusion), 9 (just an equal number of pairwise edge disjoint paths and edges whose removal disconnects the source and the sink);   4.4/2b.
8 We Nov 1 4.1/2ab, 4a.
Bonus problem:
  1. Prove that Floyd's algorithm (see section 4.1) finds the shortest distances between all pairs of vertices.
7 Mo Oct 23 Bubble sort (5,1,3,4,2);   3.4/1a, 4c (for 1a only, provided heap in class, see this pdf file);   4.2/2,4,8.
6 Mo Oct 16 3.1/2,6,31ac;   3.2/2,4,12ab, 20.
Bonus problem:
  1. Express the degree of each vertex using the adjacency matrix.
5 We Oct 4 1.4/18;   2.4/2,4,8.
Bonus problems:
  1. Find the chromatic polynomial of a cycle of length n.
  2. Show that for maps with disconnected countries no fixed number of colors suffices to color all maps.
4 We Sep 27 2.3/2ab, 10ab;   2.4/14abcd.
Our first test is on Monday, September 25. You may download the Sample Test 1 to prepare for it.
3 We Sep 20 2.1/2,4,10;   2.2/2ac, 4bcp, 16.
Bonus problems:
  1. 2.1/8
  2. Prove Grinberg's theorem
2 We Sep 13 1.4/2,8,20.
Bonus problem (2pts), expires when this assignment is due: Find the theorem in the book (page number, theorem number) stating the number of edges of a tree.
1 We Sep 6 1.1/2ab, 6a, 8, 16a;   1.2/2,4,6fbh;   1.3/2,6,16
Bonus questions:
  1. The Petersen graph is shown in the picture below.
    Show that the Petersen graph may also be defined as the graph whose vertices are all 2-element subsets of {1,2,3,4,5} with an edge connecting {i,j} and {k,l} exactly when {i,j} and {k,l} are disjoint.
  2. Prove that the edge graph of the n-dimensional hypercube is bipartite. (The vertices of the n-dimensional hypercube are all binary strings of length n, two vertices are adjacent when exactly one of their coordinates differs.)