The deadlines do not apply to the Bonus questions,
which expire only once we solve them in class, or on November 25 at
latest.
Notation: 5.1/8a means exercise 8, part a, in chapter 5,
section 1.
| No. |
Date due: |
Problems: |
| 13 |
Mo Nov 25 |
2.4/14e; 3.3/2
Bonus: Show that for maps with disconnected countries no fixed
number of colors suffices to color all maps. (B09, 5 points)
|
| 12 |
Mo Nov 18 |
4.5/4b (Start with the spanning tree solution using the NW corner
rule. Contact me if you missed class and want to double-check your
solution to the last assignment.) 2.4/6,12.
Bonus question: Prove Lemma 2 on page 170 using algebra
only. (B08, 3 points)
|
| 11 |
Mo Nov 11 |
4.5/3,4 (only find the initial spanning tree solution
using the NW corner rule. Ignore the cost matrices).
Board problem: Write the doubly stochastic matrix
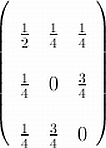 as a convex combination of permutation matrices.
as a convex combination of permutation matrices.
|
| 10 |
Mo Nov 4 |
4.4/2b,8. |
| 9 |
Mo Oct 28 |
4.3/6,9,16.
|
| 8 |
Mo Oct 21 |
4.2/2 (you may use the solution of 4.2/1, provided at the end of the
book) ,4,8; 4.3/2b: show as much detail as seen in class. In
particular, I need all slack graphs (flows may be omitted), all
augmenting paths, with the least capacity along the path marked, the
final flow, the corresponding minimum cut (not any minimum cut, but the
one computed by the algorithm), and the final flow value.
|
| 7 |
Mo Oct 14 |
bubble sort (5,1,3,4,2); 3.4/1a,4c; 4.1/2ab, 4a.
|
| 6 |
We Oct 9 |
3.1/31a, 31c; 3.2/2,4 (visit vertices in increasing order of
numbering, just like in Example 1),12ab,20.
Bonus question:
- Express the degree of a vertex in terms of the adjacency matrix
(B07, 3 points)
- Describe how you can find out whether a graph is connected, based on
its adjacency matrix, using only matrix addition and
multiplication. (B08, 5 points)
|
| 5 |
Mo Sep 30 |
3.1/2,4,6,10,16.
Bonus question: Find the chromatic polynomial of a cycle of
length n. Prove your statement by induction. (B06, 5 points.)
|
| 4 |
Mo Sep 23 |
2.3/2ab, 10ab; 2.4/2,4,8, 2.4/14cd (use the recurrence shown in
class at least once, or you will get no credit).
|
| 3 |
Mo Sep 16 |
2.1/2,4,10; 2.2/2ac, 4bcp, 16.
Bonus questions:
- 2.1/8 (B03, 5 points)
- Prove that the hypercube graph has a Hamilton circuit (B04, 5
points)
- Prove Grinberg's theorem (B05, 5points)
|
| 2 |
We Sep 11 |
1.4/2,8,20.
|
| 1 |
We Sep 4 |
1.1/2ab, 6a, 8, 16a; ; 1.2/2,4,6fbh; 1.3/2,6,16.
Bonus questions:
- Prove that the edge graph of
the n-dimensional hypercube is bipartite. (The vertices of
the n-dimensional hypercube are all binary strings of
length n, two vertices are adjacent when exactly one of their
coordinates differs.) (B01, 5 points)
- The Petersen graph is shown in the picture below.
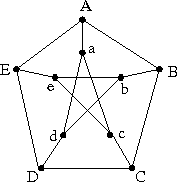 Show that the Petersen graph may also be defined as the graph whose
vertices are all 2-element subsets of {1,2,3,4,5} with
an edge connecting {i,j} and {k,l} exactly when
{i,j} and {k,l} are disjoint. (B02, 5 points)
Show that the Petersen graph may also be defined as the graph whose
vertices are all 2-element subsets of {1,2,3,4,5} with
an edge connecting {i,j} and {k,l} exactly when
{i,j} and {k,l} are disjoint. (B02, 5 points)
|

