Ward's Minimum-Variance Method
This is a statistical method that merges attributes into clusters based on the
residual error within the differences of the instance attributes from those of an
other instance or group. This method tries to minimize the variance of the differences
in attributes within a cluster using the distance algorithm based on the sum of
squares of the difference of the attributes. It joins cluster pairs whose merger
minimizes the increase in the total sum of squares within-group error.
We have not found a description on how SAS handles nominal variables in this method.
It is our assumption that each attribute value is one distance away from the next
in ascending order as specified in the data.
A more scientific description of this method is shown below, taken from the SAS
documentation:
The following method is obtained by specifying METHOD=WARD. The distance between
two clusters is defined by:
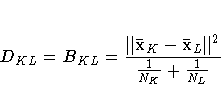 If d(x,y) = (1/2) | x - y |2,
then the combinatorial formula is:
DJM = [((NJ + NK) DJK + (NJ +
NL) DJL - NJDKL) / (NJ + NM)]
In Ward's minimum-variance method, the distance between two clusters is the ANOVA sum of
squares between the two clusters added up over all the variables. At each generation, the
within-cluster sum of squares is minimized over all partitions obtainable by merging two
clusters from the previous generation. The sums of squares are easier to interpret when
they are divided by the total sum of squares to give proportions of variance (squared
semipartial correlations).
Ward's method joins clusters to maximize the likelihood at each level of the hierarchy under
the following assumptions:
If d(x,y) = (1/2) | x - y |2,
then the combinatorial formula is:
DJM = [((NJ + NK) DJK + (NJ +
NL) DJL - NJDKL) / (NJ + NM)]
In Ward's minimum-variance method, the distance between two clusters is the ANOVA sum of
squares between the two clusters added up over all the variables. At each generation, the
within-cluster sum of squares is minimized over all partitions obtainable by merging two
clusters from the previous generation. The sums of squares are easier to interpret when
they are divided by the total sum of squares to give proportions of variance (squared
semipartial correlations).
Ward's method joins clusters to maximize the likelihood at each level of the hierarchy under
the following assumptions:
- multivariate normal mixture
- equal spherical covariance matrices
- equal sampling probabilities
Ward's method tends to join clusters with a small number of observations, and it is strongly
biased toward producing clusters with roughly the same number of observations. It is also
very sensitive to outliers (Milligan 1980).
Ward (1963) describes a class of hierarchical clustering methods including the minimum
variance method.
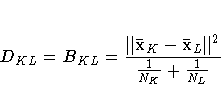 If d(x,y) = (1/2) | x - y |2,
then the combinatorial formula is:
DJM = [((NJ + NK) DJK + (NJ +
NL) DJL - NJDKL) / (NJ + NM)]
In Ward's minimum-variance method, the distance between two clusters is the ANOVA sum of
squares between the two clusters added up over all the variables. At each generation, the
within-cluster sum of squares is minimized over all partitions obtainable by merging two
clusters from the previous generation. The sums of squares are easier to interpret when
they are divided by the total sum of squares to give proportions of variance (squared
semipartial correlations).
Ward's method joins clusters to maximize the likelihood at each level of the hierarchy under
the following assumptions:
If d(x,y) = (1/2) | x - y |2,
then the combinatorial formula is:
DJM = [((NJ + NK) DJK + (NJ +
NL) DJL - NJDKL) / (NJ + NM)]
In Ward's minimum-variance method, the distance between two clusters is the ANOVA sum of
squares between the two clusters added up over all the variables. At each generation, the
within-cluster sum of squares is minimized over all partitions obtainable by merging two
clusters from the previous generation. The sums of squares are easier to interpret when
they are divided by the total sum of squares to give proportions of variance (squared
semipartial correlations).
Ward's method joins clusters to maximize the likelihood at each level of the hierarchy under
the following assumptions: