The deadlines do not apply to the Bonus questions,
which expire only once we solve them in class, or on November 27 at
latest.
Notation: 5.1/8a means exercise 8, part a, in chapter 5,
section 1.
| No. |
Date due: |
Problems: |
| 13 |
Tue Nov 25 at noon |
4.5/4b.
|
| 12 |
Tue Nov 18 at noon |
Board problem: Write the doubly
stochastic matrix
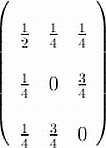
as a convex combination of permutation matrices. Show all steps!
|
| 11 |
Tue Nov 11 at noon |
4.3/16 (simplify your graph, using Dijkstra's algorithm); 4.4/2b
(use slack graphs),8.
|
| 10 |
Tue Nov 4 at noon |
4.3/6 (no need to show all your work: either show a flow that saturates
demand, or a cut whose capacity is smaller than the demand), 4.3/9.
|
| 9 |
Tue Oct 28 at noon |
4.3/2b. Show all steps. More specifically, I need: each slack graph,
each augmenting path, final flow, maximum flow value, minimum cut that
can be read from the final slack graph.
|
| 8 |
Tue Oct 21 at noon |
4.1/2a, 2b, 4a (bolden the edges that belong to the spanning tree,
write above each vertex the cost to get there from the root, and write
down the vertices in the order you added them to the spanning
tree. You do not need to compute the entire spanning tree, only the
part you need to find a minimum weight path) 4.2/2,4,8.
Bonus problem: Prove that Floyd algorithm finds the matrix of minimum costs as claimed. (B10, 5 points)
|
| 7 |
Tue Oct 14 at noon |
3.4/1a; 3.4/4c (use the heap on page 4 of the lecture notes on October 7, only sort this heap, associated to 3.4/1a);
(Mandatory) Board problem: bubble
sort (5,1,3,4,2). Show each step as in the notes
of October 7.
|
| 6 |
Tue Oct 7 at noon |
3.1/31a, 31c; 3.2/2,4,12ab,20.
|
| 5 |
Tue Sep 30 at noon |
3.1/2,4,10,16.
|
| 4 |
Tue Sep 23 at noon |
2.3/2ab, 10ab; 2.4/2,4,14cd (you have to use the recurrence stated in Theorem 6 at least once!).
Bonus: Find the chromatic polynomial of a cycle of length n. Prove your statement by induction. (B09, 5 points) |
| 3 |
Tue Sep 16 at noon |
2.1/2,4,10; 2.2/2ac, 4bc, 16.
Bonus
questions:
- 2.1/8. (B06, 5 points)
- Prove Grinberg's theorem. (B07, 5 points)
- Prove that the hypercube graph has a Hamilton circuit. (B08, 5 points)
|
| 2 |
Tue Sep 9 at noon |
1.4/2,8,20.
Bonus question: Show that for maps with disconnected countries no fixed number of colors suffices to color all maps. (B05, 5 points)
|
| 1 |
Tue Sep 2 at noon |
1.1/2ab, 6a (just give an example), 8, 16a; 1.2/2, 6bfh;
1.3/2,6.
Bonus questions:
- Describe a matrix computation that uses the adjacency matrix of a simple
graph to decide whether the graph is connected. (B01, 5 points)
- Prove that the edge graph of
the n-dimensional hypercube is bipartite. (The vertices of
the n-dimensional hypercube are all binary strings of
length n, two vertices are adjacent when exactly one of their
coordinates differs.) (B02, 5 points)
- Describe in terms of the adjacency matrix, when are two simple
graphs isomorphic (B03, 3 points).
- The Petersen graph is shown in the picture below.
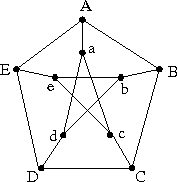 Show that the Petersen graph may also be defined as the graph whose
vertices are all 2-element subsets of {1,2,3,4,5} with
an edge connecting {i,j} and {k,l} exactly when
{i,j} and {k,l} are disjoint. (B04, 5 points)
Show that the Petersen graph may also be defined as the graph whose
vertices are all 2-element subsets of {1,2,3,4,5} with
an edge connecting {i,j} and {k,l} exactly when
{i,j} and {k,l} are disjoint. (B04, 5 points)
|

