(Mandatory) Board problems:
- Write
 as a rational function of x.
as a rational function of x. - Prove by induction that the Fibonacci numbers satisfy Fn+3=2Fn+1+Fn.
- Using the handout on forward differences, write
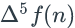 as
a linear combination
of f(n), f(n+1),
..., f(n+5).
as
a linear combination
of f(n), f(n+1),
..., f(n+5). - Using the method presented in the handout on forward differences, write f(n)=n3
as a linear combination of the binomial coefficients
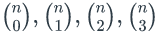 .
.
(Mandatory) Board problems:
- Prove by induction that the Fibonacci numbers satisfy 3Fn=Fn+2+Fn-2 for n ≥ 2.
- Let Tn be the number of ways to triangulate a convex n-gon with nonintersecting diagonals. Express the number Tn in terms of the Catalan numbers. Prove your statement by stating and explaining the recurrence satisfied by the numbers Tn.
- Find the coefficient of xn in
 . Express your answer in simplest form using Catalan numbers.
. Express your answer in simplest form using Catalan numbers. - How many ways are there to parenthesize the product x1x2...xn ? State your answer in terms of the Catalan numbers and explain it.
- Write the power
series
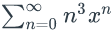 as a rational function of x.
as a rational function of x.
Bonus problems:
- Prove Napoleon's theorem, stated in the lecture notes of April 1 (B06, 8 points).
- Extend the definition of Fibonacci numbers to negative indices in such a way that they satisfy the same recurrence. State and prove a formula expressing the negative-indexed Fibonacci numbers in terms of the positive-indexed ones (B07, 5 points).
- Give a combinatorial proof of the fact that the number of partitions of n into odd parts is the same as the number of the partitions of n into distinct parts (B08, 10 points).
- Find the number p(n,2) of composition of n into 2 parts using generating functions (B09, 5 points).
- You are given n+1 copies of 1 and n-1 copies of -1 written around a circle. Prove that there is exactly one place to start summing these numbers clockwise around the circle such that the sum of the numbers added so far is always positive (B10, 5 points).
(Mandatory) Board problems:
- Find a ordinary generating function in which the coefficient of some power of x expresses the number of ways to purchase n bottles of soda when soda comes in packs of 6, 12 or 24. Indicate which power of x to look for.
- Find the ordinary generating function of for the number of nonnegative integer solutions of z1+z2+z3=15, subject to 0≤ zi≤ 8 for i=1,2,3. Also indicate the coefficient of which power of x is the answer to your question.
- Write a formula for the coefficient
of xk in
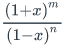 .
.
- Find a closed form formula for the sequence given by the recurrence an+2-4an+1+4an=0 and the initial conditions a0=1 and a1=4.
- Find a closed form formula for the sequence given by the recurrence an+2-2an+1+2an=0 and the initial conditions a0=1 and a1=1.
(Mandatory) Board problems:
- Find the partial fraction decomposition
of
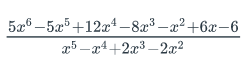 .
. - Complete the computation of a closed-from formula of the sequence given by the recurrence an+1=-an-an-1, and by the initial conditions a0=1 and a1=0. Your answer should be a linear combination of the powers of the complex third roots of unity.
Board problem: Find the coefficient of xn in
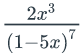 .
.
Board problem: Find the number of ternary strings of length 5 that have no two consecutive 1's.
Bonus:
- Given a partition of n by its type vector 1m12m2...nmn, describe an algorithm that computes the type vector of its conjugate. (B04, 5 points)
- Write the Stirling number of the second kind S(n,n-5) as a polynomial of n. (B05, 8 points)
(Mandatory) Board problems:
- Find the number of ways of writing 10 as a sum of three nonnegative integers. Order matters!
- Find the number of ways of writing 10 as a sum of three positive integers. Order matters!
- Find the coefficient of x11x23x31x42 in (x1+x2+x3+x4)7.
(Mandatory) Board problems:
- Prove by induction that n < 2n holds for all positive integers n.
- How many ways are there to select five coins out of an unlimited supply of pennies, nickels, dimes and quarters?
Bonus: Extend Vandermonde's identity (Theorem 4.7) to the case when m and n are not integers, and are replaced with variables x and y respectively. (B03, 10 points, you may want to use that a nonzero polynomial in one variable has only finitely many roots).
(Mandatory) Board problem:
Prove by induction that 13+ 23 + ... + n3 =(1+2+...+n)2 holds for all positive integer n.Bonus:
- Prove 13+ 23 + ... + n3 =(1+2+...+n)2 without using induction. (B01, 5 points).
- 1/28 (B02, 5 points).