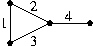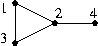No more homework will be assigned this semester. The December 5 deadline
will be strictly enforced!
| No. |
Date due: |
Problems: |
| 12 |
Mo 12/5 |
Answer 5/6 for n=6 only. (Draw an example with six colors, and
number the vertices in the order they are colored using the greedy
algorithm.)
Number the vertices in the graph G below such that each vertex
is preceded by less than col(G) vertices:
 Find the coloring number of any r-regular graph. (If you find
the question difficult, try finding the coloring number of the
3-cube first.)
Find the coloring number of any r-regular graph. (If you find
the question difficult, try finding the coloring number of the
3-cube first.)
Prove (by induction) that every odd cycle is 3-constructible.
Without using Hajós' theorem (Theorem 5.2.5) from the book prove
that every 3-constructible graph contains an odd cycle.
(Use the axioms defining a 3-constructible graph in an induction.)
|
| 11 |
Mo 11/17 |
5/2, 6/9.
Show that the dodecahedron has a 4-flow. (You may use
Proposition 6.4.5.) Find an actual 3-flow on
K3,3.
Bonus question: Draw a map of five "severely
disconnected" countries that can not be colored with less than five
colors. (Expires on Friday, Nov 21, 2003.)
|
| none |
Mo 11/10 |
Remember the test on Wednesday!
No hw assigned this week.
|
| 10 |
Mo 11/3 |
Calculate the number of H-flows of K4,
using the recursion formula (1) in the proof of Theorem 6.3.1.
Using your answer, determine the flow number of K4.
Transform the Z3-flow shown below into a
3-flow:
 Bonus question: Find a 2-flow on the edge-graph of the
octahedron.
Bonus question: Find a 2-flow on the edge-graph of the
octahedron.
|
| 9 |
Mo 10/27 |
6/2.
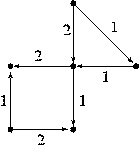
Consider the network with the capacities shown below:
 Start with this flow:
Start with this flow:
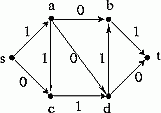 Draw the auxiliary graph, find an augmenting path and an improved
flow. Repeat until you find a flow of maximum value and a cut of minimum
value.
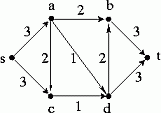
Convert the problem of finding a maximum size matching in the graph below
into a maximum flow problem:
Draw the auxiliary graph, find an augmenting path and an improved
flow. Repeat until you find a flow of maximum value and a cut of minimum
value.
Convert the problem of finding a maximum size matching in the graph below
into a maximum flow problem:
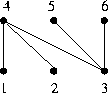 Start with the flow that corresponds to selecting the matching
consisting only of the edge {3,4}.
Start with the flow that corresponds to selecting the matching
consisting only of the edge {3,4}.
Illustrate the reduction of the "vertex version" of Menger's
theorem to the "edge" version on the graph below:
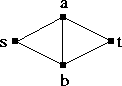
|
| 8 |
We 10/22 |
6/1. What is the dual graph of K4?
Consider the network with the capacities shown below:
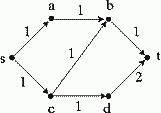 Start with this flow:
Start with this flow:
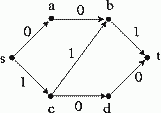 Draw the auxiliary graph, find an augmenting path and an improved
flow. Repeat until you find a flow of maximum value and a cut of minimum
value.
Draw the auxiliary graph, find an augmenting path and an improved
flow. Repeat until you find a flow of maximum value and a cut of minimum
value.
|
| 7 |
Mo 10/15 |
4/3, 4, 21, 23, 25. Prove that the Petersen graph is not planar, or draw it
as a plane graph. Find the dual graph of the 3-cube.
Bonus: What is f-e+v for connected graphs drawn on the
surface of a torus?
|
| 6 |
Mo 10/6 |
Partition the edges of the 3-cube into 3 disjoint
matchings (of maximum size). Find a maximum number of internally
disjoint paths and a minimum size vertex cut for two diametrically
opposite vertices of the cube (like (0,0,0) and
(1,1,1)).
3/6,8.
|
| 5 |
Mo 09/28 |
Remember the Test on Monday!
Find a maximum sized matching and a minimum sized cover in the
edge-graph of the 3-cube, the edge-graph of the octahedron, and
the graph below:
 Consider the graph shown on the picture below:
Consider the graph shown on the picture below:
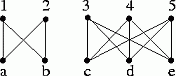 The matching M={{1,b},{3,d}, {4,e},{5,c}} is not maximum sized,
while the matching M'={{1,1}, {2,b},{3,c}, {4,d}, {5,e}}
is. Describe how to use exercise 2/1 to find an augmenting path for M.
The matching M={{1,b},{3,d}, {4,e},{5,c}} is not maximum sized,
while the matching M'={{1,1}, {2,b},{3,c}, {4,d}, {5,e}}
is. Describe how to use exercise 2/1 to find an augmenting path for M.
|
| 4 |
Mo 09/21 |
Write down the vectors belonging to the cut space of the graph below:
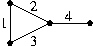 Illustrate the proof of Theorem 1.9.6 by explicitly listing the basis
vectors for the cycle space and cut space of the graph below (use the
indicated numbering of edges, and the spanning tree represented by the
bold edges):
Illustrate the proof of Theorem 1.9.6 by explicitly listing the basis
vectors for the cycle space and cut space of the graph below (use the
indicated numbering of edges, and the spanning tree represented by the
bold edges):
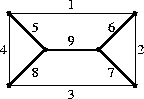
Bonus questions: Is the number of minimal cuts larger or equal to
the dimension of the cutspace?
Finish the proof of Proposition 1.9.8/part (ii) (Expires on
Monday, Sep 22, 2003.)
|
| 3 |
Mo 09/15 |
Draw a depth-first-search tree for the Petersen graph.
Decide whether either of the 3-cube and the octahedron has a
bipartite edge graph, or an Eulerian tour. (Justify your answer.)
1/20,21.
Write down the adjacency matrix of the graph shown below:
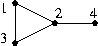
Bonus questions: Decide whether either the d-cube has a
bipartite edge graph. (Justify your answer.)
Express the degree of a
vertex in terms of the adjacency matrix.
|
| 2 | We 09/10 |
1/9 (i), 1/9 (ii) for n=3 only, 1/15, 1/16.
Bonus question: 1/9 (ii) for all n.
|
| 1 |
We 09/03 |
1/1. Draw the line graph of the Petersen graph (p. 140). Find a
maximum size independent set among the vertices of the 3-cube. Answer
all questions of 1/2 in general, except for the girth and circumference
questions, which you only need to answer for d=3. Answer 1/4 by
giving an example.
Bonus questions: Show that the Petersen graph is the complement of
the line graph of K6. Find a maximum size
independent set among the vertices of the d-cube. Find the girth and
circumference of the d-cube.
|