ARCHIVE PAGE

This page is not updated any more.

Homework assignments
(MATH 3116-001, Fall 2011)

Last update: Tuesday, November 29, 2011

Disclaimer: The information below comes with no warranty. If, due to typographical error, there is a discrepancy between the exercises announced in class and the ones below, or this page is not completely up to date, the required homework consists of those exercises which were announced in class. Check for the time of last update above. If, by my mistake, a wrong exercise shows up below, I will allow you extra time to hand in the exercise that was announced in class. If, however, exercises are missing because this page is not up to date, it is your responsibility to contact me before the due date. (No extra time will be allowed in that case.) This page is up to date if the last update happened after the last class before the next due date.

The deadlines do not apply to the Bonus questions, which expire only once we solve them in class, or on November 28 at latest.

Notation: 5.1/8a means exercise 8, part a, in chapter 5, section 1.

No.	Date due:	Problems:
13	Tu Dec 6	3.4/2, 3.4/4c. For 3.4/c you may use Mike Copley's Java applet to build a heap (note: it does not take negative numbers, so you have to "cheat"). Then apply the algorithm described in the book and shown in Figure 3.25 to sort the heap. Warning: the procedure in our book to sort the heap is different from what is shown by the applet, so only use the applet to build the heap. Show each stage of the heap while it is being sorted. Perform the algorithm only for the list given in 3.4/1b.
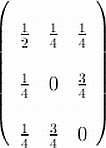
12	Tu Nov 29	4.5/4b Board problem: Write the doubly stochastic matrix as a convex combination of permutation matrices. Bonus question: Prove that no permutation matrix is the convex combination of other permutation matrices.
12	Thu Nov 17	4.4/8
11	Thu Nov 10	4.3/16; 4.4/2 (all of part b, for part a outline only how you would set up the network). The date of our second test was moved up to Tuesday November 15. We will review on Thursday November 10. You may download the Sample Test 2 I distributed in class on Thursday November 3.
10	Thu Nov 3	4.3/2b,6; 4.1/2c (you will automatically get full credit if you scored at least 90% on 4.1/2a, otherwise this is your second chance to get this method right).
9	Thu Oct 27	4.2/2,4,8. Note: While working on the exercises in section 4.2, you may want to revisit the Java applets simulating Kruskal's algorithm and Prim's algorithm (by Kenji Ikeda). Bonus problem: Explain how Floyds algorithm (see p. 129 in our textbook) works. In particular what is the role of the variable k?
8	Thu Oct 20	4.1/2ab, 4. Note: While working on the exercises in section 4.1, you may want to revisit the Java applets simulating Dijkstra's algorithm (by Kenji Ikeda).
7	Thu Oct 13	3.2/2,4,12ab (use 17 for 12a),20,24. Bonus problems: How can you find the degree of a vertex using the adjacency matrix? (Justify your answer.) Find and prove a formula for the chromatic polynomial of a circuit C_n of length n.
6	Thu Oct 6	3.1/29ac.
5	Thu Sep 29	2.4/4,8,14. Note: 2.4/8a has a typo. The correct inequality is: 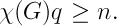. Our first test is on Tuesday September 27. You may downloand the Sample Test 1 I distributed in class on Thursday September 22.
4	Thu Sep 22	2.2/2ac, 4ado, 6, 16 (use Grinberg's theorem); 2.3/2ae, 8ab.
3	Thu Sep 15	2.1/2,4,10; 1.4/20. Bonus problems: Show that allowing disconnected countries no fixed number of colors suffices to color all maps. Prove Grinberg's theorem.
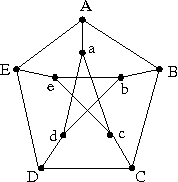
2	Thu Sep 8	1.3/2, 4, 10; 1.4/2,4,8. Board problem: The Petersen graph is shown in the picture below. Show that the Petersen graph may also be defined as the graph whose vertices are all 2-element subsets of {1,2,3,4,5} with an edge connecting {i,j} and {k,l} exactly when {i,j} and {k,l} are disjoint. Bonus problem (2pts), expires when this assignment is due: Find the theorem in the book (page number, theorem number) stating the number of edges of a tree.
1	Thu Sep 1	1.1/2ab, 6a, 8, 16a; 1.2/2,4,6aeg. Bonus problem: Prove that the edge graph of the n-dimensional hypercube is bipartite. (The vertices of the n-dimensional hypercube are all 01-strings of length n, two vertices are adjacent when exactly one of their coordinates differs.)