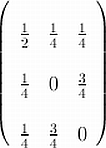
Board problem: Write the doubly stochastic matrix
Bonus problem:
- Prove that Floyd's algorithm (see section 4.1) finds the shortest distances between all pairs of vertices.
Bonus problem:
- Express the degree of each vertex using the adjacency matrix.
Bonus problems:
- Find the chromatic polynomial of a cycle of length n.
- Show that for maps with disconnected countries no fixed number of colors suffices to color all maps.
Our first test is on Monday, September 25. You may download the Sample Test 1 to prepare for it.
Bonus problems:
- 2.1/8
- Prove Grinberg's theorem
Bonus problem (2pts), expires when this assignment is due: Find the theorem in the book (page number, theorem number) stating the number of edges of a tree.
Bonus questions:
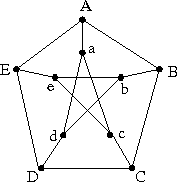
- The Petersen graph is shown in the picture below.
- Prove that the edge graph of the n-dimensional hypercube is bipartite. (The vertices of the n-dimensional hypercube are all binary strings of length n, two vertices are adjacent when exactly one of their coordinates differs.)