The deadlines do not apply to the Bonus questions,
which expire only once we solve them in class, or on November 29 at
latest.
Notation: 5.1/8a means exercise 8, part a, in chapter 5,
section 1.
| No. |
Date due: |
Problems: |
| 13 |
Mo Nov 29 at noon |
Finish 4.5/4b Start with the solution given on the first page of the lecture notes of November 22.
Bonus: Show that no permutation matrix is the convex combination of other permutation matrices (B09, 3 points). |
| 12 |
Mo Nov 22 at noon |
4.5/3,4: Only find the spanning tree solution using the NW corner
rule. Do not continue!
Board problem: Write the doubly
stochastic matrix
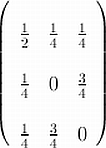
as a convex combination of permutation matrices. Show all steps!
|
| 11 |
Mo Nov 15 at noon |
4.4/2b,8. |
| 10 |
Mo Nov 8 at noon |
4.3/9,16. |
| 9 |
Mo Nov 1 at noon |
4.3/2b: show as much detail as seen in class. In particular, I need all slack graphs (flows may be omitted), all augmenting paths, the final flow, the corresponding minimum cut (not any minimum cut, but the one computed by the algorithm), and the final flow value. 4.3/6: only maximum flow and final answer are needed. |
| 8 |
Mo Oct 25 at noon |
4.1/2ab, 4a. (Bolden the edges that belong
to the spanning tree, write above each vertex the cost to
get there from the root, and write down the vertices in the
order you added them to the spanning tree. You do not need
to compute the entire spanning tree, only the part you need
to find a minimum weight path.) 4.2/2 (you may use
the solution of 4.2/1, provided at the end of the book)
,4,8.
Bonus question: Describe how you can find out whether a graph is connected, based on its adjacency matrix, using only matrix addition and multiplication. (B08, 5 points)
|
| 7 |
Mo Oct 18 at noon |
3.4/1a (draw a picture like Fig. 3.24).
3.4/4b: only perform the heap evacuation on the heap shown in the
picture:
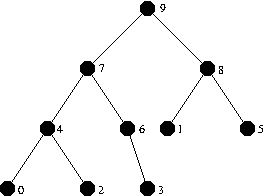
Board problem: bubble sort (5,1,3,4,2). Show each step as in the notes of October 13. |
| 6 |
We Oct 13 at noon |
3.1/10,16,31a,31c; 3.2/2,4 (visit
vertices in increasing order of numbering, just like in
Example 1),12ab,20.
Board problem:
Design a decision tree that identifies an element x
of the set {1,2...,n}, using only questions asking
whether x is less than a given number. You should
not use more than 5 levels. |
| 5 |
Mo Oct 4 at noon |
2.4/14cd (use the recurrence learned at least once, or you will get no credit!); 3.1/2,4,6.
- Show that for maps with disconnected countries no fixed number of colors suffices to color all maps. (B04, 5 points)
- Prove that the hypercube graph has a Hamilton circuit. (B05, 5 points)
- Prove Grinberg's theorem. (B06, 5points)
- Find the chromatic polynomial of a cycle of length n. Prove your statement by induction. (B07, 5 points)
|
| 4 |
Mo Sep 27 at noon |
2.3/2ab, 10ab; 2.4/2,4,8. |
| 3 |
Mo Sep 20 at noon |
2.1/2,4,10; 2.2/2ac, 4bc, 16. |
| 2 |
Mo Sep 13 at noon |
1.3/12a; 1.4/2,8,20.
|
| 1 |
We Sep 8 at noon |
1.1/6a (just state the length and give an example), 1.1/16a (list all 21
pairs, circle the ones that disconnect the graph), 1.1/8, 1.1/2a (draw
the directed graph, arrows should point towards the defeated team),
1.1/2b (list all 4!=24 possibilities, underline an adjacent
pair that violates the condition in each order that is not a
dominance order, circle the dominance orders). 1.2/2,4,6fbh;
1.3/2,6.
Bonus questions:
- The Petersen graph is shown in the picture below.
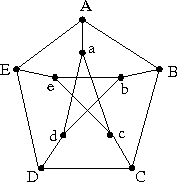Show that the Petersen graph may also be defined as the graph whose
vertices are all 2-element subsets of {1,2,3,4,5} with
an edge connecting {i,j} and {k,l} exactly when
{i,j} and {k,l} are disjoint. (B01, 5 points)
- Prove that the edge graph of the n-dimensional hypercube
is bipartite. (The vertices of the n-dimensional hypercube are
all binary strings of length n, two vertices are adjacent when
exactly one of their coordinates differs.) (B02, 5 points)
- What is the number of all possible adjacency matrices of all simple
graphs on n numbered vertices? (Keep in mind that there are
no loop edges, no multiple edges, and edges are undirected.) (B03, 5
points.)
|