ARCHIVE PAGE

This page is not updated any more.

Homework assignments
(MATH 3166-003, Spring 2021)
Instructor: Gábor Hetyei Last update: Thursday, April 22, 2021

Disclaimer: The information below comes with no warranty. If, due to typographical error, there is a discrepancy between the exercises announced in class and the ones below, or this page is not completely up to date, the required homework consists of those exercises which were announced in class. Check for the time of last update above. If, by my mistake, a wrong exercise shows up below, I will allow you extra time to hand in the exercise that was announced in class. If, however, exercises are missing because this page is not up to date, it is your responsibility to contact me before the due date. (No extra time will be allowed in that case.) This page is up to date if the last update happened after the last class before the next due date.

The deadlines do not apply to the Bonus questions, which expire only once we solve them in class, or on April 22 at latest.

Notation: 1.4/16a means exercise 16, part a, in chapter 1, section 4.

No. Date due: Problems:
12 Th Apr 29 at noon 4.4/1,3,4.
11 Th Apr 22 at noon 4.3/1 (you have to use Stirling numbers or you will get no credit), 6,9,12.
Board problem: Using the same method as for 4.3/12, find a closed formula for f(n)=12+22+...+n2. You will not get any credit if you just prove the formula by induction.
Bonus problem: Using the same method as for 4.3/12, find a closed formula for f(n)=13+23+...+n3. (B07, 10 points)
10 Th Apr 15 at noon 4.1/2a,4,5,8;   4.2/1a, 6b.
Bonus: Using the generating function method to count the triangulations of a regular polygon (on pages 148 and 149) as a guide, transform the recurrence for the Catalan numbers in our handout into a quadratic equation, solve it, and derive the closed form formula for the Catalan numbers. (B06, 10 points)
9 Tu Apr 6 at noon 3.6/2d, 6.
Bonus: 3.5/3 (B05, 5 points).
8 Tu Mar 30 at noon 3.6/4 (use the method presented in class).
Board problem:
  1. The sequence a0, a1, a2,... is given by the initial conditions a0=1 , a1=4 and by the recurrence an+2=4 · an+1-4 · an.
    Using the method shown in class, find a closed form formula for an.
7 Tu Mar 23 at noon 3.3/3be, 4, 8;   3.4/2,5,10.
6 Tu Mar 16 at noon 3.2/1b,4a,9a,10,11.
Board problems:
  1. Using the inclusion-exclusion formula, find the number of ternary strings of length 5 that have no two consecutive 1's.
  2. The sequence a0, a1, a2,... is given by the initial conditions a0=3 , a1=5 and by the recurrence an+2=4 · an+1-3 · an.
    Prove by induction that an=2+3n.
Bonus:
  • 3.1/5a (B03, 5 points)
  • 3.2/9b (B04, 5 points)
5 Tu Mar 9 at noon 2.3/11,12 (algebraic proof suffices);   2.4/8,10 (you may use Ferrers diagrams instead of type vectors, if you prefer);   3.1/2,4,11.
4 Tu Mar 2 at noon 2.3/6,9
Bonus: Using algebra, prove Pascal's formula 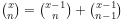in the case when x is not necessarily an integer (B05, 3 points).
3 Tu Feb 23 at noon 2.2/4ac,8,9.
Bonus: Extend Vandermonde's formula (formula (2.5) in section 2.1) to the case when m and n are not integers, and are replaced with variables x and y respectively. (B02, 10 points, you may want to use that a nonzero polynomial in one variable has only finitely many roots).
2 Tu Feb 16 at noon 1.3/12;   1.4/2,6,10,16;   1.5/2;   2.1/3,4d.
1 Tu Feb 2 at noon 1.1/6,8,10, 16;   1.2/4,8;   1.3/4.
Bonus question: 1.1/12 (B01, 5 points, you must assume each set is represented by a circle).