(Mandatory) Board problems:
- Write the function f(n)=n3
as a linear combination of the binomial coefficients
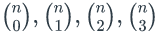 .
. - Write
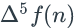 as
a linear combination
of f(n), f(n+1),
..., f(n+5).
as
a linear combination
of f(n), f(n+1),
..., f(n+5). - Write the polynomial 3x4-x3+4x+10 in the basis (x)0,(x)1, (x)2, (x)3, (x)4, using the Stirling numbers of the second kind. Simplify your answer. No credit will be given if you find your answer by any other means.
- Find the Stirling number of the second kind
S(n,2) by extracting the coefficient
of xn
from

using partial fraction decomposition. No credit will be given if you are not working with generating functions. The formula for S(n,2) may be found in the lecture notes of April 21.
(Mandatory) Board problems:
- Find the coefficient of xn
in

- Let Tn be the number of triangulations of a convex n-gon hat uses only noncrossing diagonals. Express the number Tn in terms of the Catalan numbers Cn. Prove your formula, by stating the (approriately shifted) recurrence formula for these numbers and explaining why this recurrence is valid.
- Write the power
series
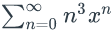 as a
rational function
of x.
as a
rational function
of x. - Write the power
series
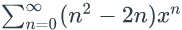 as a
rational function of x.
as a
rational function of x.
Bonus:
- You are given n+1 copies of 1 and n-1 copies of -1 written around a circle. Prove that there is exactly one place to start summing these numbers clockwise around the circle such that the sum of the numbers added so far is always positive. (B08, 5 points).
(Mandatory) Board problems:
- Find a generating function in which the coefficient of some power of x expresses the number of ways to purchase n bottles of soda when soda comes in packs of 6, 12 or 24. Indicate which power of x to look for.
- Find a generating function in which the coefficient of some power of x expresses the number of solutions of the equation z1+z2+z3=15 satisfying 0≤ zi≤ 8 for i=1,2,3. Indicate which power of x to look for.
- Write a formula for the coefficient of xk in

- Use the formula
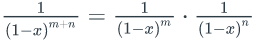 to write
a formula for
to write
a formula for
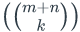 . Then also give a
combinatorial proof for that formula.
. Then also give a
combinatorial proof for that formula.
Bonus:
- Find a direct combinatorial proof for the final answer of Example 8.6. (B06, 5 points.)
- Use generating functions to find a formula for p(n,2) , that is, the number of partitions of n into 2 parts. Then also give a direct explanation of your formula. (B07, 5 points).
(Mandatory) Board problem:
- Prove by induction that the Fibonacci numbers satisfy 3Fn=Fn+2+Fn-2 for n ≥ 2.
8/51.
(Mandatory) Board problems:
- Find a closed form formula for the sequence given by the recurrence an+2-4an+1+4an=0 and the initial conditions a0=1 and a1=4.
- Find a closed form formula for the sequence given by the recurrence an+2-2an+1+2an=0 and the initial conditions a0=1 and a1=1.
(Mandatory) Board problems:
-
Find the partial fraction decomposition of
Hint: x=1 is a root of the denominator.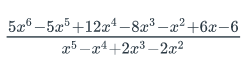 .
. - Find the coefficient of xn in
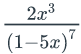 .
.
(Mandatory) Board problem:
- Use the sieve formula to find the number of set partitions of [n] that have no singleton block.
- Find the number of ternary strings of lenth 5 that have no two consecutive 1's.
(Mandatory) Board problem: Prove that composing a permutation with a transposition changes the number of inversions by an even number. (Work out the 9 cases discussed in class on February 20.)
Bonus: Write the Stirling number of the second kind S(n,n-5) as a polynomial of n. (B05, 8 points)
Bonus: Given a partition of n by its type vector 1m12m2...nmn, describe an algorithm that computes the type vector of its conjugate. (B04, 5 points)
(Mandatory) Board problem: Find the coefficient of x11x23x31x42 in (x1+x2+x3+x4)7.
(Mandatory) Booard problems:
- Find the number of ways of writing 10 as a sum of three nonnegative integers. Order matters!
- Find the number of ways of writing 10 as a sum of three positive integers. Order matters!
- How many ways are there to select five coins out of an unlimited supply of pennies, nickels, dimes and quarters?
Bonus: prove Pascal's identity
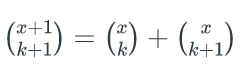
using algebra, allowing the value of x to be non-integer. Here
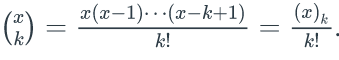 . (B02, 3 points)
. (B02, 3 points)
Bonus: Extend Vandermonde's identity (Theorem 4.7) to the case when m and n are not integers, and are replaced with variables x and y respectively. (B03, 10 points, you may want to use that a nonzero polynomial in one variable has only finitely many roots).
Bonus: 1/27 (B01, 5 points)