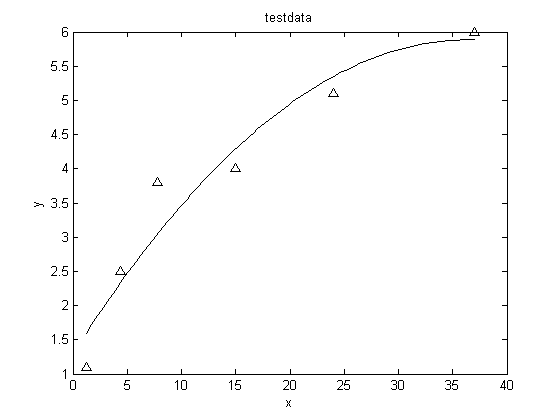
function plot_excel_data % © J. M. Hill S2011 % read data from excel file into a matrix, plot designated columns as % discrete points, overlay plot of curve fit % user must edit code for correct values of filename, xcol, ycol, n % and plot title and labels clc; %clear command window filename = 'test.xlsx'; xcol = 2; %column xcol in the a matrix will be read into vector x ycol = 4; %column ycol in the a matrix will be read into vector y [x,y] = read_excel_cols(filename,xcol,ycol); %read colmuns from excel file plot_data(x,y) %-------------------------------------------------------------------------- function [x,y] = read_excel_cols(filename, xcol, ycol) c = xlsread(filename); % read all the data in the file into array a x = c(:,xcol); % assign all numbers in col xcol to vector x y = c(:,ycol); % assign all numbers in col ycol to vector y [n,m] = size(c); %determine size, n rows, m columns b = c(:,m); %strip b vector out of c matrix for i = 1:n for j = 1:n a(i,j) = c(i,j);%strip a matrix out of c matrix end end %alternatively: a = c(:,1:n) can replace the loop; write_matrix_screen(n,a,b) %-------------------------------------------------------------------------- function write_matrix_screen(n,a,b) for i = 1:n for j = 1:n fprintf(1,'%3.2g ',a(i,j)); %write coefficient matrix to screen end fprintf(1,'%3.2g\n',b(i)); %write right-hand-side vector to screen end %-------------------------------------------------------------------------- function plot_data(x,y) %plot x-y pairs, overlay plot of curve fit plot(x,y,'k^') hold on % overlay plots n = 2; % order of polynomial regression (max = 3) c = polyfit(x,y,n); % fit x-y pairs with polynomial of order n ypred = polyval(c,x); % predictions dev = y - mean(y); % deviations - measure of spread SST = sum(dev.^2); % total variation to be accounted for resid = y - ypred; % residuals - measure of mismatch SSE = sum(resid.^2); % variation NOT accounted for Rsq = 1 - SSE/SST; % percent of error explained (r-squared) fprintf(1,'r-squared = %g\n',Rsq) for i = 1:n+1 fprintf('c(%d)= %6.4g\n',i,c(i)); %print polynomial coefficients end m = numel(x); %determine the number of elements in vector x dx = (x(m)-x(1))/100; %calculate a delta-x equal to (last_x - first_x)/100 xx = x(1):dx:x(m); %divide x scale into 100 ptsto make a good plot switch n case 1 %linear fit line = c(1).*xx + c(2); case 2 %second-order fit line = c(1).*xx.^2 + c(2).*xx + c(3); case 3 %cubic fit line = c(1).*xx.^3 + c(2).*xx.^2 + c(3).*xx + c(4); otherwise disp('Cannot do fit greater than 3 with this code'); end plot(xx,line,'k') ylabel('y') xlabel('x') title('testdata') hold off %quit overlaying plots
6 1.2 5 1.1 1 1 NaN 7 4.4 6 2.5 2 2 NaN 6 7.8 8 3.8 3 3 NaN 7 15 5 4 4 4 NaN 6 24 3 5.1 5 5 NaN 7 37 1 6 6 6 NaN r-squared = 0.935904 c(1)= -0.003445 c(2)= 0.2515 c(3)= 1.296