Problem Statement:

Design and build a beam that can withstand an evenly distributed point load. This structural beam can either be a hollow box beam, an “I” beam, or an “H” beam. The beam must withstand an x-axis load of 375 pounds and a y-axis load of 150 pounds. On the x-axis, the beam cannot deflect more than 0.230 inches. On the y-axis, the beam cannot deflect more than 0.200 inches. The maximum amount of weight the beam can be is 250 grams and cannot cost more than $10.50. The total span of the beam must be 18 inches. Calculate the most efficient beam that meets the requirements.

Safety Factor Information:

A safety factor is commonly used in engineering and can be defined simply as the value that accounts for any mistakes in calculations or material quality. When the safety factor is applied to load it adds to it. Therefore, if a safety factor of 1.3 is required, in the calculation 30% of the load would be added to the total. The best explanation of the value is when the stress in the model remains much inferior to the strength of the material, the safety factor stays superior to 1 and the model is “safe” (Cyprien 2016). Each beam has different strengths and weaknesses, this is something I had to consider when including factor of safety. The value I chose for the factor of safety was 1.3 because it is a realistic constituent while calculating the beam. The design requirements provided limit us as students to design a beam that will have little deflection. I had to use the load value given and apply the factor of safety on both the x-axis and y-axis to culminate a final answer for how efficient the beam will be. While testing, there are other modes of failure that a beam under loading may experience. One influence of beam failure is cracking, there are several different types of cracks that occur. Some examples of the cracks are shear, torsional, corrosion, and shrinkage cracks before failure (Prasad 2020). While making the beam there can be errors in construction, that can result in failure. If the material used isn’t of certain quality, it wouldn’t matter how perfect the design is it can still fail. User error could occur where the person testing the beam doesn’t take proper measures when setting up the beam and results in breakage. In conclusion I can use the safety factor in my calculations to limit the possibility of my beam failing.

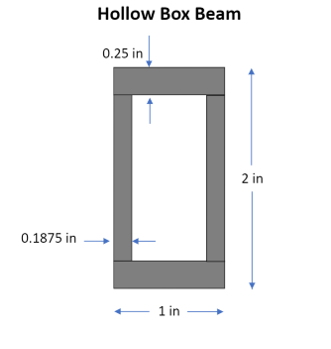
A safety factor of 1.5 was used to calculate the deflection. The deflection of the beam on the x-axis equaled 0.095 in with 375 lbf and on the y-axis equaled 0.138 in with 150 lbf. The cross-section of the beam follows a 2:1 height to base ratio. The weight of the beam is 174.091 g. The walls are made of two 3/16 in * 1 ½ in pieces. The top and bottom are made of two ¼ in * 1 pieces in. The total price equals $10.48 and meets all the requirements.

Decision Matrix:

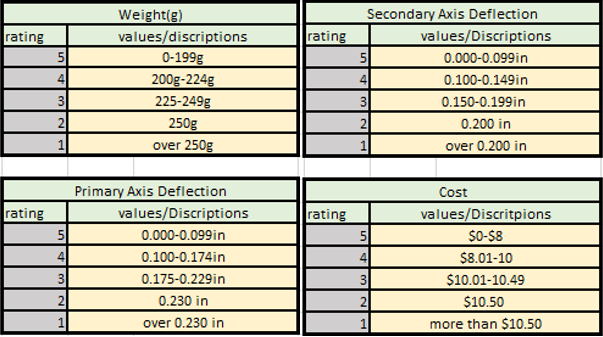
The evaluation criteria for determining how good the beams are consisted of the weight, axis deflections, and cost. As a group we concluded that only having the four criteria was enough to deduce which beam is used. We decided that the primary axis deflection should have the highest weight of the criteria because if it fails, we fail. The secondary axis deflection is also important but we can still be graded if we fail on this axis. The weight of the beams determines if we can use it or not. To use the beam it has to be under 250 grams. The cost is the least important of the criteria at 10% because we didn’t have to worry about it as much when designing the beams until the end.

The following picture is how we determined the rating for each criteria of the beam:

Bill of Materials:

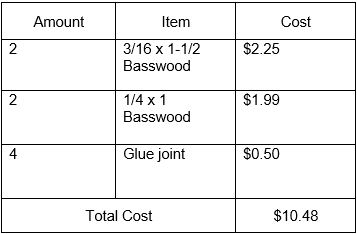
In conclusion, our team selected my hollow box beam design for building and testing. It had the highest score on the decision matrix and it follows the 2:1 ratio suggested by our proffessor. This beam meets every requirement including the safety factor of 1.5.

Bellow is our team constructing the beam.

Bellow is our beam completed.