Problem Statement:

Given a resistor diagram consisting of five different resistor combinations, voltage output of each combination, total voltage, and the total current through the circuit. The total voltage of the circuit is 18 volts, and the total current is 0.0009 amperes. The first resistor combination has 18 volts going in and 15.162 volts going out. Resistor combination number two has 15.162 volts going in and 6.079 volts going out. Resistor combination number three has 6.079 volts going in and 5.559 volts going out. Resistor combination number two has 5.559 volts going in and 1.259 volts going out. The final resistor combination has 1.259 volts going in and 0 volts going out.

To complete the circuit, the resistors provided have values of 10,000, 3,300, 2,200, 330, and 220 ohms (Ω). The circuit must have at least one parallel resistor combination. The gold band on the resistor means the values are within plus or minus five percent of the value.

We must calculate what combination of resistors will equate to the voltage drops between each node. Calculate the voltage drop by subtracting the voltage going into the resistors minus the voltage going out. Using a breadboard and sets of resistors, you must calculate the resistor combinations to equal 0 volts at the end.

Theory:

To complete this project, we must use Ohm’s law and Kirchhoff’s Voltage law. Ohm’s law consists of three variables used to calculate either voltage, resistance, or current in a circuit. The equation is V = IR, you can change these variables to solve for unknown values. Kirchhoff’s Voltage law states that the sum of the voltage differences around any closed loop in a circuit must be zero. This law can be used to calculate the resistance values in our project for the separate nodes.

Methods:

To design the voltage divider circuit, we must use Kirchhoff’s Voltage law. I approached this problem by creating a calculator in Microsoft Excel. In my calculator I could enter in the values of the input or output voltages, and it would tell me how much resistance I would need. To calculate the resistance needed, I entered in values of the resistors and checked until I had a value close to the solution. I could have manually done all these calculations to check which resistors to use, but I found using a calculator made the process easy. I double checked my calculations using Ohm’s law to make sure the resistance values could be used to equal the voltage and current.

Final Circuit Drawing:

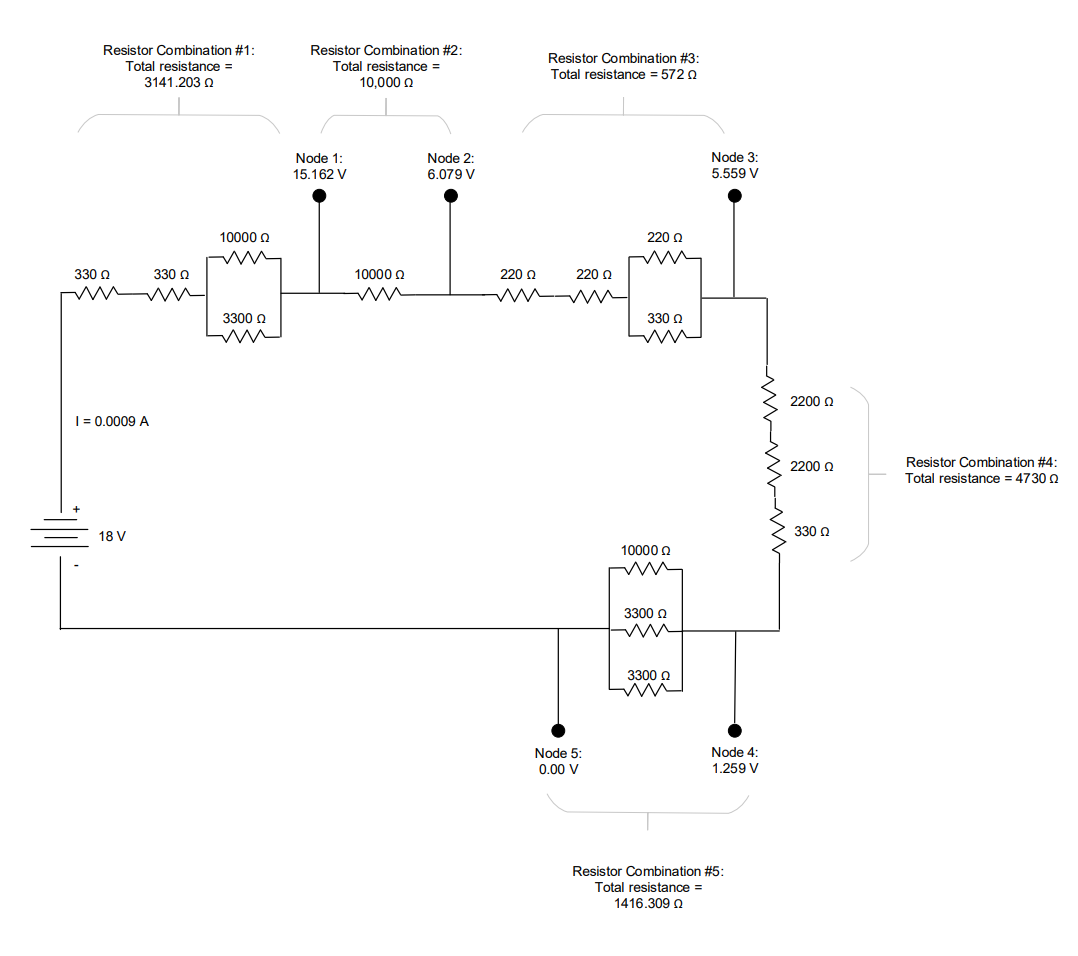
Results:

The circuit values that were calculated were very close to the values given. I was able to achieve this by trial and error. Once I found a result that satisfied my needs, I would move on to the next resistor combination. Through resistor combination #1, the difference between theoretical and experimental values was -0.48%. Resistor combination #2 was similar and the difference between the values was -1.5%. For the third combination, I achieved a value that was almost perfect; The differenced between the theoretical versus the experimental was -0.072%. The following resistor combination had a difference of -1.69%, which is still an impressive value, but could’ve been better. The outcome of the combination could’ve been closer to the value I was trying to get but due to space limitations on the bread board, I could not. My last resistor combination was perfect only since it had to get to 0.00 V. Overall the circuit was very consistent and did not stray from the five percent requirement.

Some of the values I had to achieve were very small. For example, resistor combination #2 had a voltage drop of 0.52 V. To get within five percent of this small value, I had to use resistors in series and in parallel. This process took a long time but eventually I was able to develop a successful combination.

I recommend spending lots of time testing different resistor combinations when you approach this project. I found it helpful to make a calculator on excel, just like the beam calculator. You can assume that these resistors won’t get the theoretical values perfectly; therefore, I would attempt making combinations closest to the values I want.

Conclusion:

The electrical project’s main objectives are to develop a circuit with separate nodes that dissipate the voltage through each node. Given the circuit and each voltage after each node, we can calculate which resistors will equal the output. The resulting values of the final circuit were all within the five percent range of the given node values. No alternative nodes were needed after testing.