ARCHIVE PAGE

This page is not updated any more.

Homework assignments
(MATH 3116-001, Fall 2005)
Instructor: Gábor Hetyei Last update: Monday, November 28, 2005

Disclaimer: The information below comes with no warranty. If, due to typographical error, there is a discrepancy between the exercise numbers announced in class and the numbers below, or this page is not completely up to date, the required homework consists of those exercises which were announced in class. Check for the time of last update above. If, by my mistake, a wrong exercise number shows up below, I will allow you extra time to hand in the exercise whose number was announced in class. If, however, exercise numbers are missing because this page is not up to date, it is your responsibility to contact me before the due date. (No extra time will be allowed in that case.) This page is up to date if the last update happened after the last class before the next due date.

Notation: 1.1.2 means the second exercise in the first section of the first chapter.

The deadlines do not apply to the Bonus questions, which expire only once we solve them in class, or on December 2 at latest.

No. Date due: Problems:
14 We Nov 9 9.1.2, 9.1.6.
13b Mo Nov 28 Bonus: Assume that the eigenvalues of the graph G1 are r1, ..., rm and that the eigenvalues of the graph G2 are s1, ..., sn. Prove that the eigenvalues of the Cartesian product of G1 and G2 are all numbers of the form ri+sj. (Hint: Use the very first bonus question below, from assignment 1).
Bonus: Using the statement in the previous bonus question, find the eigenvalues of the (3-dimensional) cube.
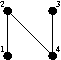13 Mo Nov 28 5.4.3: (i) for Figure 5.6, find only the cycle space for Figure 5.7 (c). 5.5.5: Find the fundamental cycles and cuts for the following spanning trees:
and 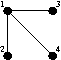for K4,
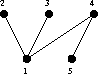
for K2,3. (One part is {1,5} the other is {2,3,4}.)

Bonus: Denote the incidence matrix of a graph by B (the columns are indexed by the edges) and its transpose by BT. Prove that BBT differs from the adjacency matrix only on its diagonal, and describe the difference.
12 Mo Nov 14 5.1.1 (ii), 5.1.4 (correct the question to dim V=4), 5.1.5, 2.3.4 (ii).
11 We Nov 9 12.5.4.
10 Mo Oct 31 12.2.4 questions (ii)-(vi) for both networks. 12.4.3 for Fig 12.13 on page 171 (note that the max flow and the min cut values are in the back of the book as the solution of 12.2.5, but you have to show how the algorithm finds them).
No new hw assigned on Friday. Review for the next test will be on Monday, but I already distributed a Sample Test 2.
9 Mo Oct 24 "Board" questions (not in the book):
  1. Find the dual of the graph shown in the picture:
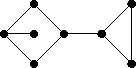
  2. Prove that in a self-dual planar graph there is at least one vertex of degree 3.

From the book: 12.1.2, 12.1.3, 12.1.5 (i) and (ii), 12.1.6.
Bonus: 1.2.1.5 (iii)
Draw a map of six (disconnected) countries that can not be colored with less than six colors. For even more bonus points, explain how to draw a map of n countries that can not be colored with less than n colors.
8 We Oct 19 8.2.1, 8.2.3.
7 We Oct 12 7.3.1, 7.3.3 (i)-(iii), 7.3.5, 7.3.6, 7.3.7/(i), (iv), (viii), 7.4.7.
6 Mo Oct 3 7.1.2, 7.1.4, 7.1.5, 7.1.7.
Bonus: Prove that the edge graph of an n-dimensional hypercube is bipartite.
5 Mo Sep 26 4.2.5 (i), 4.3.3 (i).
Bonus: Assume T and T' are trees on the same vertex set, with edge sets {e1, e2, ..., ev-1} and {f1, f2, ..., fv-1}, respectively. Assume that e1=f1, e2=f2, ..., ei-1=fi-1 but ei is not an edge of T'. We know that then ei, together with some edges fi1, fi2, ..., fikfrom T', forms a cycle. Prove that at least fij may be added to {e1, e2, ...,ei-1} without forming a cycle.
No new was homework assigned on Friday Sep 23. Remember the test on Monday. If you missed the class on Friday, download the Sample Test 1 I distributed.
4 Mo Sep 19 3.2.2, 3.2.5/(i), (ii), 3.3.3, 4.1.1, 4.1.2, 4.1.4 (prove only that in a tree there is a unique path between any two vertices- the other implication was shown in class).
To complete the proof of Theorem 3.5, prove the following:
Lemma: Assume the positive integers x, y and v satisfy x+y=v. Prove that then xy is greater than or equal to v-1.
Bonus: Prove that (iii) implies (iv) in Theorem 3.3.
3 Mo Sep 12 2.4.1, 2.4.3, 2.5.6, 3.1.1, 3.1.4 (i).
2 We Sep 7 2.1.3 (cycles of length 8 and 9 only), 2.1.5, 2.1.7 (i); finish 2.1.1 (solution in the back of the book is incorrect), 2.2.3 (ii), 2.3.2
Note: In Exercise 2.2.3 (ii), the weight of the edge sc is missing. Assume it is 10.
1 Mo Aug 29 1.1.2, 1.1.4 (iii) and (iv), 1.2.3, 1.2.8 (i), (iii) and (vi), 1.2.9, 1.3.2.
Bonus: 1.1.7; describe the adjacency matrix of the Cartesian product of two graphs.