The purpose of cluster analysis is to place observations into groups or clusters suggested by the data such that observations in a given cluster tend to be similar to each other in some sense, and objects in different clusters tend to be dissimilar. We want to cluster customers to illustrate the similarities of customers with one type of credit card and to discern the differences of customers that have other types of credit cards.

Conceptual clustering is a form of clustering that, given a set of unlabeled objects, produces a classification scheme over the objects. The COBWEB Algorithm was chosen for this task. COBWEB generates hierarchical clustering; where clusters are described probabilistically. The hierarch is constructed incrementally. At each node in the hierarchy, COBWEB considers adding the instance to that existing node or creating a new node. A two step process occurs:

• First COBWEB using the categorical utility, determines if the instance can 'fit' into an existing cluster or if another cluster must be built. The category utility is a probability function of attribute pairs existing in 2 different instances, so that the similarity of attribute values within a cluster and dissimilarity of attribute values between clusters both increase. The characterization of clusters, the probability of each attribute's value within the cluster, will give some advantage in predicting the values of the class attributes of instances in that cluster.
• Next, the derived concept descriptions/characterizations of that cluster are updated.

The COBWEB algorithm used was implemented in the Weka Toolkit.

The data must be presented to Weka formatted as an .arff file. This attributes are listed and attributes defined at the start of the .arff file. The data follows as comma separated values. In the Weka explorer environment, load data set using the Preprocess mode tab.

Clustering is initiated via the Cluster mode tab, where a clustering algorithm is selected. Options selected were Classes to Clusters option, selecting CardType as the class attribute. These cause the CardType attribute to be ignored during the clustering process. In a perfect world, each cluster would define a specific CardType. Without knowledge of the CardType, the algorithm would build a cluster whose characterizations would define clearly one of the CardTypes and the probability of that CardType value in that cluster would be 100%.

To evaluate the COBWEB clustering the class (CardType) values of instances within each cluster is used. To compute the classes-to-cluster error, the distribution of the class (CardType) values within the cluster is calculated. If the majority of the class is GOLD, then the CardTypes JUNIOR and CLASSIC in that cluster are in error. Consider a cluster has 10 instances: 8 GOLD, 1 CLASSIC, 1 JUNIOR. The percentage of instances incorrectly clustered is 20%. The percentage of instances correctly clustered is 80%.

In Weka this is done as follows:

• After the clustering algorithm completes, right click on the last line in the result list window.
• Next, choose Visualize cluster assignments. The Weka cluster visualize window appears.
• Click Save. Weka saves the cluster assignments in and .arff file. To show the cluster assignments, Weka adds a new attribute, Cluster, and includes its corresponding values at the end of each data line. Only the leaf clusters labels are saved.
• To examine clusters at higher levels in the hierarchy, leaf clusters and other lower level clusters can be combined.

The COBWEB algorithm was run twice. Once with a cutoff value of 0.18 and once with a cutoff value of 0.17. This was because Weka returns the cluster information only for the leaf clusters and prunes the tree by levels. So to see the cluster information for clusters at different levels, we had to run the clustering algorithm twice.

The results of the COBWEB Clustering analysis are interpreted in the following chart (click the light green boxes to see the percentages of attribute values within each selected cluster).

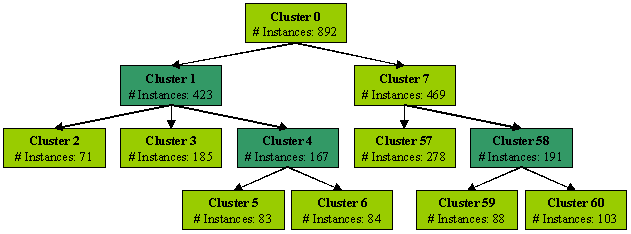We then looked at the probabilities of the attributes in each cluster and compared and contrasted them. From that we inferred descriptions of customer characteristics for different card-type holders. The entire cluster information table can be viewed here. Below is a subset of selected attributes:

Description	All Card Holders	Cluster 2	Cluster 3	Cluster 5	Cluster 6	Cluster 7	Cluster 57	Cluster 59	Cluster 60
Number of Instances	892	75	182	83	83	469	277	94	83
Percentage Distributions within Clusters by AGE
Youth	21.00%	12.00%	0.00%	98.00%	0.00%	20.00%	0.00%	100.00%	0.00%
Adult	21.00%	24.00%	0.00%	0.00%	94.00%	19.00%	0.00%	0.00%	93.00%
Middle Age	56.00%	60.00%	100.00%	0.00%	0.00%	59.00%	100.00%	0.00%	0.00%
Senior	2.00%	4.00%	0.00%	1.00%	6.00%	2.00%	0.00%	0.00%	6.00%
Percentage Distributions within Clusters by GENDER
Female	47.00%	100.00%	100.00%	100.00%	100.00%	0.00%	0.00%	0.00%	0.00%
Male	53.00%	0.00%	0.00%	0.00%	0.00%	100.00%	100.00%	100.00%	100.00%
Mean Value of AVERAGE BALANCE
Mean	51653.23	54304.88	51668.22	46762.24	51136.43	52179.92	53217.44	48965.39	51136.43
Std. Deviation	11109.32	12241.39	9367.23	13780.03	10064.00	10983.18	11055.47	11241.49	10064.01
Median	51292.00	54205.72	51580.11	43661.80	50401.42	51449.19	52323.52	48804.16	50401.42
Percentage Distributions Within Clusters by NUMBER OF USERS PER ACCOUNT
Single	83.00%	0.00%	100.00%	100.00%	100.00%	83.00%	82.00%	88.00%	100.00%
Joint	17.00%	100.00%	0.00%	0.00%	0.00%	17.00%	18.00%	12.00%	0.00%
Percentage Distributions Within Clusters by CARDTYPE
Junior	17.00%	10.00%	0.00%	74.00%	1.00%	16.00%	0.00%	78.00%	1.00%
Classic	74.00%	80.00%	91.00%	21.00%	88.00%	73.00%	86.00%	18.00%	88.00%
Gold	10.00%	10.00%	9.00%	4.00%	11.00%	11.00%	13.00%	3.00%	11.00%

By voting, the most instances of a certain CardType determines the cluster class characterization. The highlighted CardType percentage represents the percentage of correctly classified instances.

Profiling the clusters descriptively

It was hard to characterize information about clusters that helped describe or define the level of card holders in our database. The Cardtype attribute values presented the table above vary not as significantly as we had hoped. There are tendencies in clusters between a Junior-Classic card group and a Classic-Gold card group:

• Clusters 2 and 7 are representative of the general card holding population.

  Cluster 2 is all Female and Cluster 7 is all Male. Cluster 2, females, average balance is somewhat higher than both the general population and the male population, but within one standard deviation. Note that Cluster 7 in the hierarchy, represents ALL male account owners. The male population is representative of the general card holder population and then clustered after that.

  If the account is a joint account for a female account owner, it is likely to be in Cluster 2.

• Clusters 3 and 57 are middle aged CLASSIC card holders

  Only the significance of the age being Middle-aged helps distinguish these clusters from Cluster 0 or the general card holder population.

• Clusters 5 and 59 are the young JUNIOR card holders

  These clusters are characterized by age=Youth and the average balance less than that of the cluster 0.

• Clusters 6 and 60 are Young adult CLASSIC card holders

  These clusters are characterized by age=Young Adult and with having a single account, i.e., do not have any other users associated with the account.

• There are not specific clusters that can be characterized as describing gold card members.

The distinction of each cluster was not obvious beyond the coupling of age group and card type. To further investigate the characteristics of customers, we ran another clustering analysis using partitioning methods. We used the SAS Enterprise Miner product. SAS uses a partitioning clustering tool implementing the WARD (Minimum variance) method. SAS takes an EXEL file as input.

There were 31 clusters identified. Below is a subset of clusters selected because they clearly distinguish differences in our attribute of interest, the card type.

Description	All Card Holders	Cluster 1	Cluster 2	Cluster 4	Cluster 6	Cluster 19	Cluster 21
Percentage Distributions within Clusters by AGE
Youth	21.00%	80.00%	18.18%	17.65%	62.50%	0.00%	0.00%
Adult	21.00%	0.00%	18.00%	11.76%	0.00%	100.00%	50.00%
Middle Age	56.00%	20%	63.64%	70.59%	37.50%	0.00%	50.00%
Senior	2.00%	0.00%	0.00%	0.00%	0.00%	0.00%	0.00%
Percentage Distributions within Clusters by GENDER
Female	47.00%	20.00%	45.45%	29.41%	37.50%	0.00%	50.00%
Male	53.00%	80.00%	54.55%	70.59%	62.50%	100.00%	50.00%
Mean Value of AVERAGE BALANCE
Mean	51653.23	26887.36	75684.47	73667.43	30521.51	78237.63	80549.51
Std. Deviation	11109.32	328.09	508.51	579.88	601.73	0.00%	909.67
Minimum	0.00%	26522.30	74787.91	72794.25	29640.67	78237.63	79906.27
Maximum	0.00%	27362.37	76453.60	7424.22	31253.80	78237.63	81192.75
Percentage Distributions Within Clusters by NUMBER OF USERS PER ACCOUNT
Single	83.00%	80.00%	54.55%	70.59%	100.00%	100.00%	100.00%
Joint	17.00%	20.00%	45.45%	29.41%	0.00%	0.00%	0.00%
Percentage Distributions Within Clusters by CARDTYPE
Junior	16.00%	60.00%	9.09%	11.76%	62.50%	0.00%	0.00%
Classic	74.00%	20.00%	45.45%	47.06%	37.50%	100.00%	100.00%
Gold	10.00%	20.00%	45.45%	41.18%	0.00%	0.00%	0.00%

By voting, the most instances of a certain CardType, determines the cluster class characterization. The highlighted CardType percentage represents the percentage of correctly classified instances. Cluster 4 is an exception. Even though GOLD does not have the largest count of instances in the cluster, it is significantly higher than that of the general population or Cluster 0.

Profiling the clusters descriptively

• Clusters 2 and 4 are significantly GOLD card users.

  They are characterized by a high average balance in their account.

• Clusters 19 and 20 are CLASSIC card users.

  What is interesting about these accounts is that they seem to be anomalies. It appears that only 3 instance were used in defining these accounts. These accounts have a significantly high average balance. That appears to be what has singled out the instances in these clusters.

• Clusters 1 and 6 are significantly JUNIOR card users

  These are characterized by a younger age and a lower average balance in their accounts.

• The remaining clusters can be generally described as follows: All have a majority of CLASSIC cards. Those with an average balance less than the Cluster 0 have more JUNIOR cards. Those with an average balance greater than Cluster 0 have more GOLD cards.